 Das ist eine nonillion, eine 1 mit 54 nullen. Das ist eine nonillion, eine 1 mit 54 nullen.
1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000
Zahlennamen
In diesem Artikel geht es um den Aufbau von Zahlennamen und die Benennung von Zahlen im Dezimalsystem.
|
Inhaltsverzeichnis
[Verbergen]
- 1 Der Aufbau von Zahlennamen
- 1.1 Die Null
- 1.2 Eins bis Neun
- 1.3 Zehn
- 1.4 Elf und Zwölf als Ausnahmen
- 1.5 Dreizehn bis Neunzehn
- 1.6 Zwanzig bis Neunzig
- 1.7 Hunderter
- 1.8 Tausender
- 1.9 Million und Milliarde
- 1.10 Billion, Billiarde und darüber hinaus
- 2 Silbenkonstruktion für beliebig große Zahlen
- 3 Zusammenstellung der Unregelmäßigkeiten
- 4 Nichtdezimale Zahlennamen
- 5 Brüche
- 6 Siehe auch
- 7 Anmerkungen
- 8 Weblinks
|
//
Der Aufbau von Zahlennamen [Bearbeiten]
Am Beispiel der Zahl vierhundertsiebenundzwanzigtausendfünfhundertvierunddreißig
(427.534) kann man den abgestuften Aufbau der Zahlennamen ersehen.
Auffällig ist dabei in der Deutschen Sprache die Umkehrung bei Zehner-
und Einerstelle, die in anderen Sprachen (zum Beispiel im Englischen)
maximal bis zur 19 vorkommt.
Die Null [Bearbeiten]
Die Null ist ein abstraktes Konzept und bezeichnet die Eigenschaft, dass von einer Entität keine Vertreter vorhanden sind. In keiner Zahl, die sich aus einer Kombination von Zahlennamen aufbaut, kommt die Null vor. Diese Bezeichnung stammt vom lateinischen nullus = keiner oder nihil = nichts.
Eins bis Neun [Bearbeiten]
Diese ersten neun Zahlen sind zugleich Ziffern: eins, zwei, drei, vier, fünf, sechs, sieben, acht, neun.
Zehn [Bearbeiten]
Aus dem urgermanischen Wort tehun, das unter anderem mit griechisch deka (δεκα) und lateinisch decem verwandt ist, hat sich über althochdeutsch zehan das heutige Wort zehn entwickelt.
Elf und Zwölf als Ausnahmen [Bearbeiten]
Elf und zwölf von gotisch¹) ainlif und twalif mit der Nachsilbe -lif
(= „das übrig bleibende“ oder „das darüber hinausgehende“). Auch in
anderen verwandten Sprachen, beispielsweise im englischen (eleven,
twelve) oder niederländischen (elf, twaalf), gibt es diese Ausnahmen.
Hier merkt man den früheren Ansatz für ein auf zwölf Zahlen basierendes
Zahlensystem. Siehe auch Dutzend (= 12), Schock (fünf Dutzend = 60) und das Gros (zwölf Dutzend = 144).
Dreizehn bis Neunzehn [Bearbeiten]
Im Gegensatz zu den Zahlen über Zwanzig, bei denen die Einerstelle und die Zehnerstelle mit einem „und“ verknüpft werden (siebenundzwanzig), entfällt dies bei den Zahlen zwischen dreizehn und neunzehn. Bei den Zahlen sechzehn und siebzehn wird die Einerstelle verkürzt ausgesprochen („sechzehn“ statt „sechszehn“ und „siebzehn“ statt „siebenzehn“).
Zwanzig bis Neunzig [Bearbeiten]
Zwanzig: von gotisch¹) twai tigjus (= „zwei zehn-Einheiten“), später twai tig. Diese Bildungsform setzt sich bis neunzig fort.
In manchen Sprachen sind noch Reste eines Vigesimalsystems erhalten: Zum Beispiel im Französischen) ist diese Reihe nur bis 60 nach diesem Muster aufgebaut. Danach folgen „sechzig-und-zehn“ (soixante-dix), „vier-mal-zwanzig“ (quatre-vingt) und „vier-mal-zwanzig-und-zehn“ (quatre-vingt-dix). Allerdings gibt es im Schweizer und im belgischen Französisch abweichend für 70, 80 und 90 die Zahlworte septante, huitante und nonante.
Wie schon in der Einleitung erwähnt, schert die deutsche Sprache, im
Gegensatz zu anderen Sprachen wie der russischen, ukrainischen,
englischen oder französischen, in der Reihenfolge der Zehner- und
Einer-Namen aus. Wo z. B. im Englischen die Zehnereinheit zuerst kommt
(twenty-five), wird im Deutschen die Einereinheit zuerst genannt
(fünfundzwanzig). Weitere Sprachen, in denen Einer- und Zehnernamen wie
im Deutschen gereiht werden, sind das Niederländische, das Dänische,
das Luxemburgische, das Slowenische und eben das Arabische. Im
Tschechischen sind beide Varianten möglich, d.h. „Zwanzig und eins“
oder „Einundzwanzig“.
Hunderter [Bearbeiten]
Hundert: von gotisch¹) hunda und lateinisch centum. Ursprünglich nur als Mehrzahlwort verwendet, das heißt, erst ab zweihundert. Das erste Hundert wurde noch bis ins Mittelhochdeutsche durch das Zahlwort zehan tig („zehnzig“) abgeschlossen. Um ein Mehrfaches von Hundert auszudrücken, wird eine einstellige Zahl vor die Hundert angehängt. So ist der Zahlname für das dreifache von Hundert Dreihundert. Wenn das Mehrfache von Hundert größer als 9 ist, dann wechselt man zum
Tausender [Bearbeiten]
von gotisch¹) thusundi.
Für Zahlen über Einhundert hat sich im indogermanischen Sprachraum
keine einheitliche Bezeichnung entwickelt. Der Wortstamm „Tausend“
kommt nur im germanischen, slawischen und baltischen Sprachraum vor,
während im romanischen die Bezeichnung von lateinisch mille hergeleitet ist und im griechischen von χιλιοι.
Million und Milliarde [Bearbeiten]
Million: von lateinisch mille (= tausend) und -one (vergrößerndes Suffix); also eigentlich „Großtausend“. Die Million ist das Quadrat der Tausend.
Die Milliarde ist die dritte Potenz zur Tausend oder auch tausend Millionen.
Billion, Billiarde und darüber hinaus [Bearbeiten]
Ab einer Milliarde wiederholt sich das Schema -illion und -illiarde. Die Präfixe leiten sich aus dem Lateinischen ab: Bi- für 2 (Billion und Billiarde), Tri- für 3, Quadri- für 4, Quinti- (auch: Quinqui-) für 5 und so weiter. Sie geben also Potenzen der Million an: eine Billion ist eine Million zum Quadrat, eine Trillion ist 1.000.0003, eine Quadrillion ist 1.000.0004 und so weiter. Eine Billiarde ist tausend Billionen. Das gleiche Schema lässt sich auf Trilliarde, Quadrilliarde und so weiter anwenden. Dieses System wird als logarithmisches Zillionensystem bezeichnet. Es geht auf Nicolas Chuquet und Jacques Peletier du Mans zurück.
Zahl
Zahlenname
Vorsilbe
Nachsilbe
Potenz
103N
| 1 |
Eins |
|
- |
Million0.0
|
= 100 |
| 1.000 |
Tausend |
|
- |
Million0.5
|
= 103 |
| 1.000.000 |
Million |
Mi |
-llion |
Million1.0
|
= 106 |
| 1.000.000.000 |
Milliarde |
Mi |
-lliarde |
Million1.5
|
= 109 |
| 1.000.000.000.000 |
Billion |
Bi |
-llion |
Million2.0
|
= 1012 |
| 1.000.000.000.000.000 |
Billiarde |
Bi |
-lliarde |
Million2.5
|
= 1015 |
| 1.000.000.000.000.000.000 |
Trillion |
Tri |
-llion |
Million3.0
|
= 1018 |
| 1.000.000.000.000.000.000.000 |
Trilliarde |
Tri |
-lliarde |
Million3.5
|
= 1021 |
| 1.000.000.000.000.000.000.000.000 |
Quadrillion |
Quadri |
-llion |
Million4.0
|
= 1024 |
| 1.000.000.000.000.000.000.000.000.000 |
Quadrilliarde |
Quadri |
-lliarde |
Million4.5
|
= 1027 |
| 1.000.000.000.000.000.000.000.000.000.000 |
Quintillion2 |
Quinti1 |
-llion |
Million5.0
|
= 1030 |
| 1.000.000.000.000.000.000.000.000.000.000.000 |
Quintilliarde2 |
Quinti1 |
-lliarde |
Million5.5
|
= 1033 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000 |
Sextillion |
Sexti |
-llion |
Million6.0
|
= 1036 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Sextilliarde |
Sexti |
-lliarde |
Million6.5
|
= 1039 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Septillion |
Septi |
-llion |
Million7.0
|
= 1042 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Septilliarde |
Septi |
-lliarde |
Million7.5
|
= 1045 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Oktillion |
Okti |
-llion |
Million8.0
|
= 1048 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Oktilliarde |
Okti |
-lliarde |
Million8.5
|
= 1051 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Nonillion |
Noni |
-llion |
Million9.0
|
= 1054 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Nonilliarde |
Noni |
-lliarde |
Million9.5
|
= 1057 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Dezillion |
Dezi |
-llion |
Million10.0
|
= 1060 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Dezilliarde |
Dezi |
-lliarde |
Million10.5
|
= 1063 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Undezillion |
Undezi |
-llion |
Million11.0
|
= 1066 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Undezilliarde |
Undezi |
-lliarde |
Million11.5
|
= 1069 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Duodezillion |
Duodezi |
-llion |
Million12.0
|
= 1072 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Duodezilliarde |
Duodezi |
-lliarde |
Million12.5
|
= 1075 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Tredezillion |
Tredezi |
-llion |
Million13.0
|
= 1078 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Tredezilliarde |
Tredezi |
-lliarde |
Million13.5
|
= 1081 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Quattuordezillion |
Quattuordezi |
-llion |
Million14.0
|
= 1084 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 |
Quattuordezilliarde |
Quattuordezi |
-lliarde |
Million14.5
|
= 1087 |
Silbenkonstruktion für beliebig große Zahlen [Bearbeiten]
Man ersetze 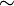 durch durch ![\it gin[t]\,](http://upload.wikimedia.org/math/5/3/e/53ee83d3789fb3c90360db2d015acd20.png) , ,  durch durch ![\it milia[t]\,](http://upload.wikimedia.org/math/3/c/4/3c4b9918c0623819b82bdf9de4aa17a9.png) , ,  durch durch  und und 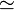 durch durch  . .
Jede natürliche Zahl  lässt sich in der Form lässt sich in der Form  schreiben, wobei schreiben, wobei  und und  ist. Die Zahl ist. Die Zahl  hat den Namen hat den Namen  für für 
heißt  für für  , und hat für , und hat für  den Namen den Namen

Dabei ist  ein Textoperator, der nacheinander jedes ein Textoperator, der nacheinander jedes  , welches unmittelbar hinter einem , welches unmittelbar hinter einem  steht, löscht, steht, löscht,  durch durch  und und  durch durch  ersetzt und den Anfangsbuchstaben in einen Großbuchstaben umwandelt. ersetzt und den Anfangsbuchstaben in einen Großbuchstaben umwandelt.
So ist zum Beispiel  eine Dezillion eine Dezillion  . .
und  eine Zentilliarde eine Zentilliarde  . .
Beispiele [Bearbeiten]
Vigintillion (1020*6 = 10120)
Septenquadragintilliarde (107*6+4*60+3=10285), (106*47+3=10285)
Zentseptuagintilliarde (101*600+7*60+3=101.023)
Die größte bekannte Mersenne-Primzahl 232.582.657-1 (Stand: Februar 2007) entspricht ca. 1,24*109.808.357 oder ca. 12 Miliamiliaseszentquattuortriginmiliaseptingentsexvigintillionen.
In der Liste besonderer Zahlen sind weitere Bezeichnungsweisen jener großen Zahlen zu finden. Eine mögliche Systematik verwendet die folgenden Vorsilben:
Dezi-
Undezi-
Duodezi-
Tredezi-
Quattuordezi-
Quindezi-
Sexdezi-
Septendezi-
Oktodezi-
Novendezi-
| 1060, 1063 |
1066, 1069 |
1072, 1075 |
1078, 1081 |
1084, 1087 |
1090, 1093 |
1096, 1099 |
10102, 10105 |
10108, 10111 |
10114, 10117 |
Viginti-
Unviginti-
Duoviginti-
Treviginti-
Quattuorviginti-
Quinviginti-
Sexviginti-
Septenviginti-
Oktoviginti-
Novenviginti-
| 10120, 10123 |
10126, 10129 |
10132, 10135 |
10138, 10141 |
10144, 10147 |
10150, 10153 |
10156, 10159 |
10162, 10165 |
10168, 10171 |
10174, 10177 |
Triginti-
Untriginti-
Duotriginti-
Tretriginti-
Quattuortriginti-
Quintriginti-
Sextriginti-
Septentriginti-
Oktotriginti-
Noventriginti-
| 10180, 10183 |
10186, 10189 |
10192, 10195 |
10198, 10201 |
10204, 10207 |
10210, 10213 |
10216, 10219 |
10222, 10225 |
10228, 10231 |
10234, 10237 |
Quadraginti-
Unquadraginti-
Duoquadraginti-
Trequadraginti-
Quattuorquadraginti-
Quinquadraginti-
Sexquadraginti-
Septenquadraginti-
Oktoquadraginti-
Novenquadraginti-
| 10240, 10243 |
10246, 10249 |
10252, 10255 |
10258, 10261 |
10264, 10267 |
10270, 10273 |
10276, 10279 |
10282, 10285 |
10288, 10291 |
10294, 10297 |
Seit dem 17. Jahrhundert gibt es zwei unterschiedliche Konventionen für Namen großer Zahlen wie Billion und Trillion:
- Das oben beschriebene (seit dem 15. Jahrhundert attestierte) ursprüngliche System der langen Leiter ist das anerkannte Referenzsystem. Es wird weltweit verwendet. Nur sehr wenige Länder weichen davon ab.
- Das System der kurzen Leiter,
bei dem die Billion nur das 1000-fache einer Million ist. Das
tausendfache einer Billion ist dann die Trillion und so weiter. Dieses
System wird in den USA, Puerto Rico, Brasilien und der Türkei
verwendet, wobei aber im Sprachgebrauch der Türkei das Wort pinad Milliarde (109) fest verankert ist. Deswegen entspricht der europäischen Milliarde die US-amerikanische billion, der europäischen Billion die US-amerikanische trillion und so weiter. Das britische Englisch gleicht sich zunehmend dem US-amerikanischen Sprachgebrauch an. Im US-Englisch fehlen die Bezeichnungen auf die Endung -arde
(Milliarde, Billiarde, ...); im britischen Englisch werden sie nur noch
selten verwendet, jedoch spricht man in England verstärkt wieder von
„tausend Millionen“ und „tausend Billionen“. Mehr zur Entstehung dieses
Systems ist im Artikel Billion zu finden.
Im veränderten System der kurzen Leiter entsprechen die Vorsilben
den Potenzen der Zahl 1000, jedoch ist die lateinische Bedeutung der
Vorsilbe stets um 1 zu klein – eine Billion sind also 10003, eine Trillion 10004.
Zusammenstellung der Unregelmäßigkeiten [Bearbeiten]
- Für Einer, Zehner und Hunderter verwendet man unterschiedliche lateinische Silben
- Es wird erst die Hunderter-, dann die Einer- und dann die Zehnersilbe genannt
- Es gibt zusätzliche Spezialvorsilben für bestimmte Zahlen
- Es wird zwischen den Nachsilben on und arde hin und hergewechselt
- Steht hinter dezi ein t, muss es gelöscht werden
- Steht gint bzw. miliat unmittelbar vor der Endung illion oder illiarde, wird der letzte Buchstabe t geschrieben, ansonsten nicht
- Bei den lateinischen Vorsilben muss tt und ii zu t bzw. i verkürzt werden
- Elf, zwölf anstatt einszehn, zweizehn (bzw. zehneins, zehnzwei)
- Bei sechzehn und siebzehn sowie sechzig und siebzig ist die Einersilbe verkürzt
- Zwanzig anstatt zweizig
- Zahlen wie z. B. einundzwanzig sind mit „und“ verknüpft
- Bei einer Zahlenzusammensetzung wie einsund zwanzig muss das s gestrichen werden
- Man verwendet die Nachsilbe zig anstatt zehn
- Die Nachsilbe ßig bei dreißig anstelle von zig stellt eine Ausnahme dar
- Die Zahl wird in Dreiergruppen eingeteilt und dementsprechend benannt
- Es wird das Dezimalsystem³) verwendet
In der Interlinguistik ist man bemüht, eine Grammatik aufzustellen, die so einfach wie möglich ist. Dennoch wurden in der Plansprache Esperanto die oben genannten Unregelmäßigkeiten nur teilweise beseitigt (siehe Numeralego).
Nichtdezimale Zahlennamen [Bearbeiten]
Der einzige heute noch benutzte Zahlenname in der deutschen Sprache, der nicht dem Dezimalsystem entstammt, ist „Dutzend“ (12). Früher wurden auch „Schock“ (60) und „Gros“ (144) verwendet, siehe auch Alte Maße und Gewichte.
Brüche [Bearbeiten]
Konstrukte der Bruchrechnung werden mit der Nachsilbe „-tel“ gebildet. Ein Ausnahme hiervon bildet zwei, zu der das Wort „Halbe“ existiert. Eins („Eintel“ in Zusammensetzungen), sieben („Siebtel“) und acht („Achtel“) verlieren eine Endung, drei („Drittel“) ändert den Stammvokal.
Weitere Ausnahmen bilden die Zahlen auf -zig, -ßig, -hundert, -tausend,
deren Bruchnenner auf „-stel“ enden, ebenso wie Millionstel,
Milliardstel usw.
Siehe auch [Bearbeiten]
- Zahlensystem
- Römische Ziffern
- Numerologie
- Vorsätze für Maßeinheiten
- Zahlwort
- Schreibweise von Zahlen
- Zahlen in unterschiedlichen Sprachen
- Liste besonderer Zahlen
- Verein Zwanzigeins
|
|
Wiktionary: Übersicht der Zahlen – Bedeutungserklärungen, Wortherkunft, Synonyme und Übersetzungen |
Anmerkungen [Bearbeiten]
¹) Die Formulierung „von gotisch ...“ ist hier als Kurzform von „aus dem Germanischen, verwandt mit gotisch ...“ zu verstehen.
²) Quinquillion und Quinquilliarde sind ebenfalls gebräuchlich.
³) Ein Computer verwendet bei seinen internen Berechnungen nicht das Dezimalsystem, sondern das Dualsystem,
weil es sich für ihn darin viel einfacher rechnen lässt. Das
Zweiersystem hat aber den Nachteil, dass für die Darstellung einer Zahl
viele Ziffern benötigt werden. Je größer die Basis b des b-adischen Stellenwertsystems
ist, desto weniger Ziffern benötigt man zur Darstellung einer Zahl.
Unter diesem Aspekt wäre es sinnvoll, b möglichst groß zu wählen, was
aber ein entsprechend größeres auswendiggelerntes Einmaleins
voraussetzt. Wichtiger für die Frage, wie schnell man damit rechnen
kann, ist allerdings, ob b viele Teiler hat oder nicht. Das
Dezimalsystem mit  stellt somit einen Kompromiss dar, welcher nicht unbedingt für alle Fälle der beste sein muss. stellt somit einen Kompromiss dar, welcher nicht unbedingt für alle Fälle der beste sein muss.
Ich bedanke mich für Ihre große Interesse an nonillion.
|